*扩展阅读：静态优化

5.3 *扩展阅读：静态优化

5.3.1 无约束的静态优化

我们首先给出无约束的静态优化的定义及相关概念。

定义 5.3.1 (无约束的静态优化) 设开集 $Ω \subseteq R^{n}$ 非空， $f : Ω \to R$ 为目标函数，无约束的静态优化问题是指求解 $max_{x \in Ω} f (x)$ 。

定义 5.3.2 (最大值点、极大值点、驻点、临界点) 称 $x^{*} \in Ω$ 为（全局）最大值点，若 $\forall x \in Ω$ ，成立 $f (x^{*}) \geq f (x)$ 。

称 $x^{*} \in Ω$ 为极大值点，若 $\exists δ > 0$ 使得 $\forall x \in B (x^{*}, δ)$ ，成立 $f (x^{*}) \geq f (x)$ 。

称 $x \in Ω$ 为驻点或临界点，若 $f$ 在 $x$ 处可微且 $\nabla f (x) = 0$ 。

为了求解无约束优化问题，我们需要借助以下定理。这些定理涉及函数的梯度，故称为一阶条件。

定理 5.3.3 (一阶必要条件) 设 $f$ 在 $x^{*}$ 处可微，若 $x^{*} \in Ω$ 为 $f$ 的极大值点（或最大值点），则 $x^{*}$ 为 $f$ 的驻点。

定理 5.3.4 (一阶充分条件) 设 $f$ 在 $Ω$ 上凹且可微， $x^{*} \in Ω$ 为 $f$ 的最大值点当且仅当 $x^{*}$ 为 $f$ 的驻点。

证明必要性：设 $x^{*}$ 为最大值点（或极大值点），则 $\exists δ > 0$ 使得 $f (x) - f (x^{*}) \leq 0, \forall x \in B (x^{*}, δ)$ 因 $f$ 在 $x^{*}$ 可微，设 $x = x^{*} + t v$ （其中 $t > 0$ 、 $v = \frac{\nabla f (x^{*})}{∥ \nabla f (x^{*}) ∥}$ ），考虑 $f$ 沿 $v$ 的方向导数，有 $∥ \nabla f (x^{*}) ∥ = \nabla f (x^{*}) \cdot v = \frac{\partial f}{\partial v} (x^{*}) = lim_{t \to 0^{+}} \frac{f (x^{*} + t v) - f (x^{*})}{t} \leq 0 ⟹ \nabla f (x^{*}) = 0$

充分性：由 $f$ 在 $Ω$ 上凹且可微，知 $f (x) \leq f (x^{*}) + \nabla f (x^{*}) \cdot (x - x^{*}) = f (x^{*}), \forall x \in Ω$ 故 $x^{*}$ 为最大值点。 $◻$

除了利用函数的梯度以外，我们还可以利用函数的Hesse矩阵来求解无约束优化问题，故称为二阶条件。

定理 5.3.5 (二阶必要条件) 设 $f$ 在 $Ω$ 上二阶连续可微， $x^{*} \in Ω$ 为 $f$ 的极大值点，则 $x^{*}$ 为 $f$ 的驻点，且 $H f (x^{*})$ 半负定。

证明由于 $f$ 在 $Ω$ 上二阶连续可微，设 $δ > 0$ ，考虑 $x^{*}$ 的邻域 $B (x^{*}, δ)$ ，由Taylor公式可得 $f (x) = f (x^{*}) + \nabla f (x^{*}) \cdot (x - x^{*}) + \frac{1}{2} (x - x^{*})^{T} H f (ξ) (x - x^{*}), ξ \in B (x^{*}, ∥ x - x^{*} ∥)$ 由一阶必要条件可得 $\nabla f (x^{*}) = 0$ 。

令 $x = x^{*} + t v$ （其中 $t > 0$ 、 $v \in R^{n}$ 满足 $∥ v ∥ = 1$ ），利用极大值点条件 $f (x) \leq f (x^{*})$ ，上式可改写为 $v^{T} H f (ξ) v \leq 0, ξ \in B (x^{*}, t), \forall v \in R^{n}, ∥ v ∥ = 1$ 令 $t \to 0^{+}$ 得到 $v^{T} H f (x^{*}) v \leq 0$ ；由于 $v$ 任意，故 $H f (x^{*})$ 半负定。 $◻$

定理 5.3.6 (二阶充分条件) 设 $f$ 在 $Ω$ 上二阶连续可微， $x^{*} \in Ω$ 为 $f$ 的驻点，则当 $H f (x^{*})$ 负定时， $x^{*}$ 为 $f$ 的极大值点。

证明由于 $f$ 在 $Ω$ 上二阶连续可微，故 $\exists δ > 0$ 使得 $H f (x)$ 在 $B (x^{*}, δ)$ 内保持负定²。由Taylor公式可得 $f (x) = f (x^{*}) + \nabla f (x^{*}) \cdot (x - x^{*}) + \frac{1}{2} (x - x^{*})^{T} H f (ξ) (x - x^{*}), ξ \in B (x^{*}, ∥ x - x^{*} ∥)$ 利用驻点条件可得 $\nabla f (x^{*}) = 0$ ；且由于 $H f (ξ)$ 负定，故当 $x \neq x^{*}$ 时，有 $(x - x^{*})^{T} H f (ξ) (x - x^{*}) < 0$ ，从而 $f (x) < f (x^{*}), \forall x \in B (x^{*}, δ), x \neq x^{*}$ 故 $x^{*}$ 为极大值点。 $◻$

对于带参数的无约束优化问题，我们有以下结论。

定理 5.3.7 (包络定理) 设 $f : Ω \times R^{k} \to R$ ，定义 $f^{*} : R^{k} \to R$ 为 $f^{*} (r) := max_{x \in Ω} f (x, r)$ ，且 $\forall r \in R^{k}$ ， $\exists x^{*} (r) \in Ω$ 使得 $f^{*} (r) = f (x^{*} (r), r)$ 。若 $f$ 在 $(x^{*} (r), r)$ 处对 $r$ 可微，且 $x^{*} (r)$ 为内点，则有 $\frac{\partial f^{*}}{\partial r_{j}} (r) = \frac{\partial f}{\partial r_{j}} (x^{*} (r), r), j = 1, 2, \dots, k$

证明考虑一个简单的情形：认为 $x^{*}$ 在 $r$ 处可微³，由链式法则可得 $\frac{\partial f^{*}}{\partial r} (r) = \frac{\partial f}{\partial x} (x^{*} (r), r) \frac{\partial x^{*}}{\partial r} (r) + \frac{\partial f}{\partial r} (x^{*} (r), r) = \nabla_{x} f (x^{*} (r), r) \cdot \frac{\partial x^{*}}{\partial r} (r) + \frac{\partial f}{\partial r} (x^{*} (r), r)$ 由一阶必要条件可得 $\nabla_{x} f (x^{*} (r), r) = 0$ ，故上式右端第一项为零，得证。 $◻$

5.3.2 带等式约束的静态优化

定义 5.3.8 (带等式约束的静态优化) 设开集 $Ω \subseteq R^{n}$ 非空， $f, g_{i} : Ω \to R$ ， $i = 1, 2, \dots, m$ 。带等式约束的静态优化问题是指求解 $max_{x \in Ω} f (x) s.t. g_{i} (x) = 0, i = 1, 2, \dots, m .$ 其中 $S = {x \in Ω ∣ g (x) = 0}$ 称为可行域（其元素称为可行解）。

同样地，我们也可以借助一阶必要条件来求解带等式约束的静态优化问题。

定理 5.3.9 (一阶必要条件) 设 $f, g_{i}$ 在 $Ω$ 上可微，且 ${\nabla g_{i} (x^{*})}_{i = 1}^{m}$ 线性无关，若 $x^{*} \in Ω$ 为 $S$ 的内点（以下简称内点 $x^{*} \in S$ ）且为带等式约束的最大值点，则存在唯一的 $λ_{i} \in R$ ， $i = 1, 2, \dots, m$ 使得 $\nabla f (x^{*}) = \sum_{i = 1}^{m} λ_{i} \nabla g_{i} (x^{*}) = {[\frac{\partial g}{\partial x} (x^{*})]}^{T} λ$

一阶必要条件的几何意义是：在最大值点处，目标函数 $f (x)$ 的等值线与约束曲面 $g (x) = 0$ 的等值线相切。

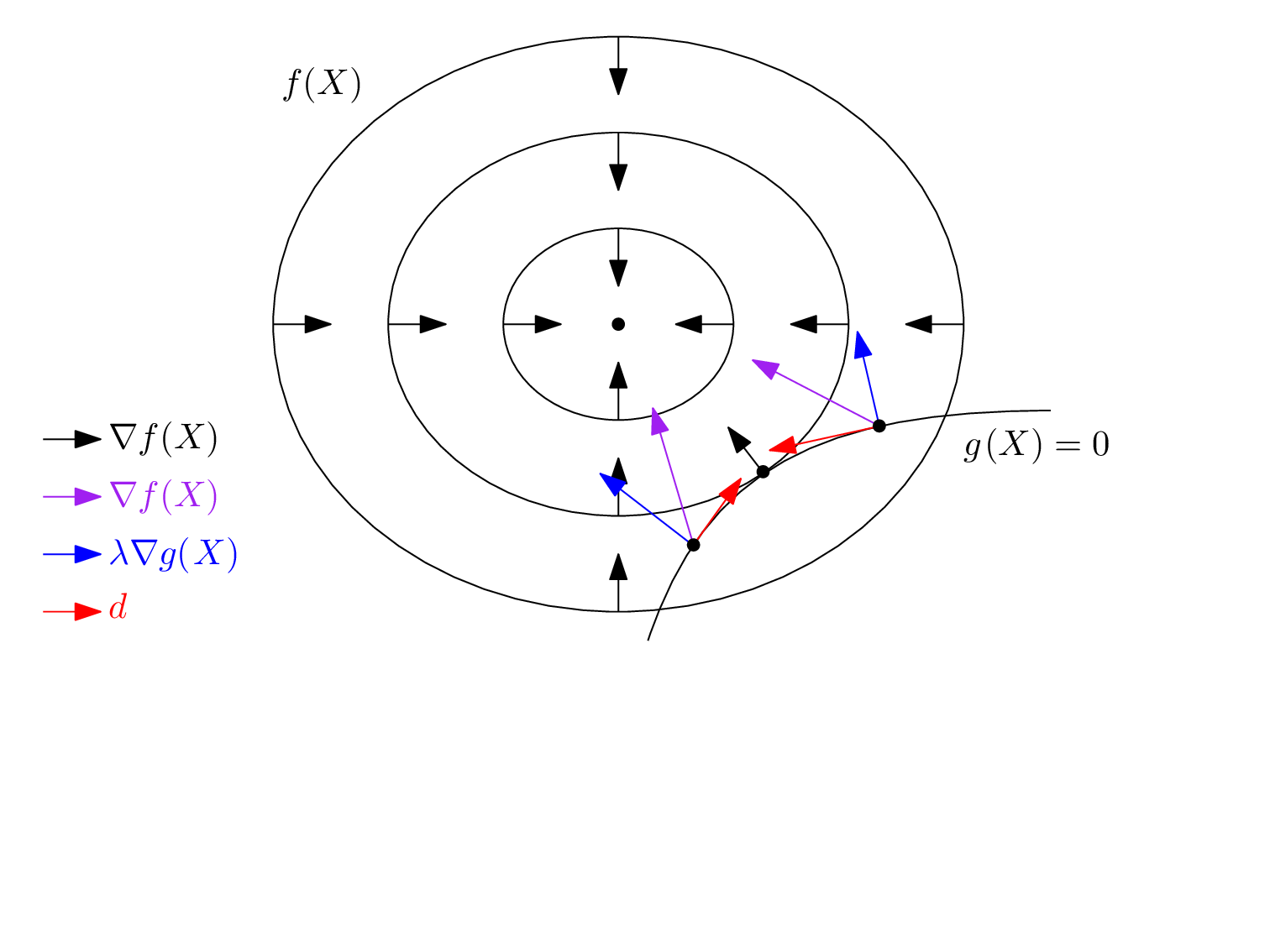
图 5.3.1: 如果上升方向 $\nabla f (x)$ 与约束曲面的法向 $λ \nabla g_{i} (x)$ 不共线，则约束曲面的切平面存在可行方向 $d$ 使得 $f$ 增大。

证明记 $u = (x_{1}, x_{2}, \dots, x_{m})^{T}$ 、 $v = (x_{m + 1}, x_{m + 2}, \dots, x_{n})^{T}$ 。由于 ${\nabla g_{i} (x^{*})}_{i = 1}^{m}$ 线性无关，对于曲面 $g (x) = g (u, v) = 0$ ，由隐函数定理可得存在内点 $x^{*}$ 的邻域 $U \subseteq S$ 、 $h \in C^{1}$ 使得 $u = h (v)$ ，且有 $\frac{\partial h}{\partial v} = - {(\frac{\partial g}{\partial u})}^{- 1} \frac{\partial g}{\partial v}$ 简而言之，在邻域 $U$ 内，约束曲面可表示为前 $m$ 个变量关于后 $n - m$ 个变量的函数， $n - m$ 称为曲面的维度。

此时带等式约束的静态优化转换为无约束静态优化。记 $F (v) = f (h (v), v)$ ，根据一阶必要条件，有 $\frac{\partial F}{\partial v} = \frac{\partial f}{\partial u} \frac{\partial h}{\partial v} + \frac{\partial f}{\partial v} = - \frac{\partial f}{\partial u} {(\frac{\partial g}{\partial u})}^{- 1} \frac{\partial g}{\partial v} + \frac{\partial f}{\partial v} = 0$ 记 $λ^{T} = \frac{\partial f}{\partial u} {(\frac{\partial g}{\partial u})}^{- 1}$ ，则 $\frac{\partial f}{\partial u} = λ^{T} \frac{\partial g}{\partial u}, \frac{\partial f}{\partial v} = λ^{T} \frac{\partial g}{\partial v} ⟹ \frac{\partial f}{\partial x} = λ^{T} \frac{\partial g}{\partial x} ⟹ \nabla f = {(\frac{\partial g}{\partial x})}^{T} λ$ $◻$

一阶必要条件的重要推论是Lagrange乘子法。

定理 5.3.10 (一阶必要条件) 设 $f, g_{i}$ 在 $Ω$ 上可微，且 ${\nabla g_{i} (x^{*})}_{i = 1}^{m}$ 线性无关，定义Lagrange函数 $L : Ω \times R^{m} \to R$ 为 $L (x, λ) := f (x) - \sum_{i = 1}^{n} λ_{i} g_{i} (x) = f (x) - λ \cdot g (x)$ 若内点 $x^{*} \in S$ 为带等式约束的最大值点，则 $\exists λ^{*} \in R^{m}$ 使得 $(x^{*}, λ^{*})$ 为 $L$ 的驻点，即 $\nabla L (x^{*}, λ^{*}) = 0$ 。由于 $\nabla_{λ} L (x^{*}, λ^{*}) = - g (x^{*}) = 0$ 自然成立，故驻点条件可简记为 $\nabla_{x} L (x^{*}, λ^{*}) = 0$ 。

同样地，如果函数 $f, g_{i}$ 满足一定的性质，我们也可以给出一阶充分条件。

定理 5.3.11 (一阶充分条件) 设 $(x^{*}, λ^{*})$ 满足一阶必要条件，且 $L (x, λ^{*})$ 关于 $x \in S$ 凹，则内点 $x^{*} \in S$ 为带等式约束的最大值点。

证明由 $L (x, λ^{*})$ 关于 $x \in S$ 凹，知 $f (x) = L (x, λ^{*}) \leq L (x^{*}, λ^{*}) + \nabla_{x} L (x^{*}, λ^{*}) \cdot (x - x^{*}) = L (x^{*}, λ^{*}) = f (x^{*}), \forall x \in S$ 即内点 $x^{*} \in S$ 为带等式约束的最大值点。 $◻$

若想仅通过 $f, g_{i}$ 的性质给出一阶充分条件，需要 $\forall λ \in R^{m}$ 都有 $L (x, λ)$ 关于 $x \in Ω$ 凹，此时不难发现：

定理 5.3.12 设 $f$ 在 $Ω$ 上可微且凹， $g_{i}$ 为线性函数，且 $(x^{*}, λ^{*})$ 满足一阶必要条件，则内点 $x^{*} \in S$ 为带等式约束的最大值点。

为了给出二阶条件，我们需要先定义约束曲面的切空间。

定义 5.3.13 (切空间) 曲面 $g (x) = 0$ 在 $x^{*}$ 处的切空间为 $T_{g} (x^{*}) := {d \in R^{n} ∣ \nabla g_{i} (x^{*}) \cdot d = 0, i = 1, 2, \dots, m}$ 。

定理 5.3.14 $T_{g} (x^{*}) = C (\frac{\partial x}{\partial v} (v^{*}))$ ，其中 $C$ 表示列空间， $v^{*}$ 满足 $x^{*} = (h (v^{*}), v^{*})$ 。

证明注意到 $\frac{\partial g}{\partial x} (x^{*}) \frac{\partial x}{\partial v} (v^{*}) = \frac{\partial g}{\partial u} (x^{*}) \frac{\partial h}{\partial v} (v^{*}) + \frac{\partial g}{\partial v} (x^{*}) = 0$ 故 $\forall d \in C (\frac{\partial x}{\partial v} (v^{*}))$ ，都有 $\frac{\partial g}{\partial x} (x^{*}) d = 0$ ，即 $C (\frac{\partial x}{\partial v} (v^{*})) \subseteq T_{g} (x^{*})$ 。

另一方面，由于 ${\nabla g_{i} (x^{*})}_{i = 1}^{m}$ 线性无关，故 $rank (\frac{\partial g}{\partial x} (x^{*})) = m$ ，从而 $\dim (T_{g} (x^{*})) = n - m$ 。

又由于 $\frac{\partial x}{\partial v} (v^{*})$ 的下 $(n - m) \times (n - m)$ 子矩阵为单位矩阵，故 $rank (\frac{\partial x}{\partial v} (v^{*})) = n - m$ 。

综上可得 $\dim (C (\frac{\partial x}{\partial v} (v^{*}))) = rank (\frac{\partial x}{\partial v} (v^{*})) = \dim (T_{g} (x^{*}))$ ，从而 $T_{g} (x^{*}) = C (\frac{\partial x}{\partial v} (v^{*}))$ 。 $◻$

设 $A$ 为 $n$ 阶对称矩阵。由于 $T_{g} (x^{*}) = C (\frac{\partial x}{\partial v} (v^{*}))$ ，故 $A$ 在切空间 $T_{g} (x^{*})$ 上半负定等价于 $d^{T} \underset{为 n - m 阶半负定矩阵}{\underset{⏟}{{[\frac{\partial x}{\partial v} (v^{*})]}^{T} A [\frac{\partial x}{\partial v} (v^{*})]}} d \leq 0, \forall d \in R^{n - m}; \frac{\partial x}{\partial v} (v^{*}) = (\begin{matrix} - {(\frac{\partial g}{\partial u} (x^{*}))}^{- 1} \frac{\partial g}{\partial v} (x^{*}) \\ I_{n - m} \end{matrix})$ 其余情况（半正定、负定、正定、不定）类同。

定理 5.3.15 (二阶必要条件) 设 $f, g_{i}$ 在 $Ω$ 上二阶连续可微， $L (x, λ) := f (x) - λ \cdot g (x)$ 。若内点 $x^{*} \in S$ 为 $f$ 限制在 $g (x) = 0$ 上的极大值点，则 $\exists λ^{*} \in R^{m}$ 使得 $(x^{*}, λ^{*})$ 为 $L$ 的驻点，且 $H_{x} L (x^{*}, λ^{*})$ 在切空间 $T_{g} (x^{*})$ 上半负定。

证明将约束曲面表示为 $u = h (v)$ 。令 $x (v) = x (v^{*} + t d)$ （其中 $t > 0$ 、 $d \in R^{n - m}$ 满足 $∥ d ∥ = 1$ ），由 $\frac{\partial x}{\partial v}$ 的连续性可得其在邻域上有界（ $\exists M, δ > 0$ 使得 $‖ \frac{\partial x}{\partial v} (η) ‖ \leq M$ 在 $η \in B (v^{*}, δ)$ 内恒成立）；再由Taylor公式可得 $x - x^{*} = t \frac{\partial x}{\partial v} (η) d, η \in B (v^{*}, t) ⟹ ∥ x - x^{*} ∥ \leq t M$ 由于 $L$ 在 $Ω$ 上二阶连续可微，设 $δ > 0$ 、 $λ^{*} \in R^{m}$ ，考虑 $x^{*}$ 的邻域 $B (x^{*}, δ)$ ，由Taylor公式可得 $L (x, λ^{*}) = L (x^{*}, λ^{*}) + \nabla_{x} L (x^{*}, λ^{*}) \cdot (x - x^{*}) + \frac{1}{2} (x - x^{*})^{T} H_{x} L (ξ, λ^{*}) (x - x^{*}), ξ \in B (x^{*}, t M)$ 由一阶必要条件可得 $\nabla_{x} L (x^{*}, λ^{*}) = 0$ 。

利用极大值点条件 $f (x) = L (x, λ^{*}) \leq L (x^{*}, λ^{*}) = f (x^{*})$ 可将上式改写为 ${[\frac{\partial x}{\partial v} (η) d]}^{T} H_{x} L (ξ, λ^{*}) [\frac{\partial x}{\partial v} (η) d] \leq 0, ξ \in B (x^{*}, t M), η \in B (v^{*}, t), \forall d \in R^{n - m}, ∥ d ∥ = 1$ 令 $t \to 0^{+}$ 可得 $d^{T} {[\frac{\partial x}{\partial v} (v^{*})]}^{T} H_{x} L (x^{*}, λ^{*}) [\frac{\partial x}{\partial v} (v^{*})] d \leq 0, \forall d \in R^{n - m}, ∥ d ∥ = 1$ 故 $H_{x} L (x^{*}, λ^{*})$ 在切空间 $T_{g} (x^{*})$ 上半负定。 $◻$

定理 5.3.16 (二阶充分条件) 设 $f, g_{i}$ 在 $Ω$ 上二阶连续可微， $L (x, λ) := f (x) - λ \cdot g (x)$ 。若 $\exists λ^{*} \in R^{m}$ 使得 $(x^{*}, λ^{*})$ 为 $L$ 的驻点，且 $H_{x} L (x^{*}, λ^{*})$ 在切空间 $T_{g} (x^{*})$ 上负定，则内点 $x^{*} \in S$ 为此规划的极大值点。

证明将约束曲面表示为 $u = h (v)$ 。令 $x (v) = x (v^{*} + t d)$ （其中 $t > 0$ 、 $d \in R^{n - m}$ 满足 $∥ d ∥ = 1$ ），由Taylor公式可得 $x = x^{*} + t \frac{\partial x}{\partial v} (v^{*}) d + \frac{t^{2}}{2} \sum_{i = 1}^{n} e_{i} d^{T} H x_{i} (η) d, η \in B (v^{*}, t)$ 由 $H x_{i}$ 的连续性可得其在邻域上有界（ $\exists M_{i}, δ > 0$ 使得 $‖ H x_{i} (η) ‖ \leq M_{i}$ 在 $η \in B (v^{*}, δ)$ 内恒成立），则有 $r (v) := x - x^{*} - t \frac{\partial x}{\partial v} (v^{*}) d ⟹ ∥ r (v) ∥ \leq t^{2} M^{'}, M^{'} = \frac{1}{2} \sum_{i = 1}^{n} M_{i}$ 由于 $L$ 在 $Ω$ 上二阶连续可微，故 $\exists δ > 0$ 使得 $H_{x} L (x, λ^{*})$ 在 $B (x^{*}, δ) \cap T_{g} (x^{*})$ 内保持负定。由Taylor公式可得 $L (x, λ^{*}) = L (x^{*}, λ^{*}) + \nabla_{x} L (x^{*}, λ^{*}) \cdot (x - x^{*}) + \frac{1}{2} (x - x^{*})^{T} H_{x} L (ξ, λ^{*}) (x - x^{*}), ξ \in B (x^{*}, t M)$ 其中 $M$ 为 $‖ \frac{\partial x}{\partial v} (v) ‖$ 在 $B (v^{*}, δ)$ 内的上界。记 $‖ H_{x} L (x, λ^{*}) ‖$ 在 $B (x^{*}, t M)$ 内的上界为 $L$ 。利用驻点条件可得 $\nabla_{x} L (x^{*}, λ^{*}) = 0$ ，代入上式可得 $\begin{aligned} L (x, λ^{*}) - L (x^{*}, λ^{*}) & = \frac{t^{2}}{2} {[\frac{\partial x}{\partial v} (v^{*}) d]}^{T} H_{x} L (ξ, λ^{*}) [\frac{\partial x}{\partial v} (v^{*}) d] + t r (v)^{T} H_{x} L (ξ, λ^{*}) [\frac{\partial x}{\partial v} (v^{*}) d] \\ + \frac{1}{2} r (v)^{T} H_{x} L (ξ, λ^{*}) r (v), ξ \in B (x^{*}, t M), v \in B (v^{*}, t) \end{aligned}$ 由于 $d \neq 0$ 、 $\frac{\partial x}{\partial v} (v^{*})$ 列满秩，故 $\frac{\partial x}{\partial v} (v^{*}) d \in T_{g} (x^{*}) ∖ {0}$ ；再由 $H_{x} L (ξ, λ^{*})$ 的负定性可得 $c (d) := - {[\frac{\partial x}{\partial v} (v^{*}) d]}^{T} H_{x} L (ξ, λ^{*}) [\frac{\partial x}{\partial v} (v^{*}) d] > 0$ 与此同时，由于 $∥ r (v) ∥ \leq t^{2} M^{'}$ ，故 $‖ r (v)^{T} H_{x} L (ξ, λ^{*}) [\frac{\partial x}{\partial v} (v^{*}) d] ‖ \leq t^{2} M^{'} L M, ‖ r (v)^{T} H_{x} L (ξ, λ^{*}) r (v) ‖ \leq t^{4} M^{' 2} L$ 因此，当 $t \leq min {\frac{c}{3 M^{'} L M}, \sqrt{\frac{2 c}{3 M^{' 2} L}}}$ 时，有 $L (x, λ^{*}) - L (x^{*}, λ^{*}) \leq \frac{t^{2}}{2} (- c + t M^{'} L M + \frac{1}{2} t^{2} M^{' 2} L) \leq - \frac{c}{6} t^{2} < 0$ 即 $L (x, λ^{*}) < L (x^{*}, λ^{*})$ ，从而 $f (x) < f (x^{*})$ 。 $◻$

若 $H_{x} L (x^{*}, λ^{*})$ 自身负定，则其在切空间 $T_{g} (x^{*})$ 上亦负定。这给了我们一个更简单的二阶充分条件。

同样地，我们也可以给出带等式约束的静态优化问题的包络定理。

定理 5.3.17 (包络定理) 设开集 $Ω \subseteq R^{n}$ 非空， $f, g_{i} : Ω \times R^{k} \to R$ ， $i = 1, 2, \dots, m$ 。定义 $S (r) = {x \in Ω ∣ g (x, r) = 0}$ ， $f^{*} : R^{k} \to R$ 为 $f^{*} (r) := max_{x \in Ω} f (x, r)$ ，且 $\forall r \in R^{k}$ ， $\exists x^{*} (r) \in S (r)$ 使得 $f^{*} (r) = f (x^{*} (r), r)$ 。定义Lagrange函数为 $L (x, λ, r) := f (x, r) - λ \cdot g (x, r)$ 记 $x^{*} (r)$ 对应的Lagrange乘子为 $λ^{*} (r)$ 。若 $f$ 在 $(x^{*} (r), r)$ 处对 $r$ 可微，且 $x^{*} (r)$ 为 $S (r)$ 的内点，则有 $\frac{\partial f^{*}}{\partial r_{j}} (r) = \frac{\partial L}{\partial r_{j}} (x^{*} (r), λ^{*} (r), r), j = 1, 2, \dots, k$

证明类似无约束情形，考虑一个简单的情形：认为 $x^{*}, λ^{*}$ 在 $r$ 处可微，由链式法则可得 $\frac{\partial f^{*}}{\partial r} (r) = \frac{\partial f}{\partial x} (x^{*} (r), r) \frac{\partial x^{*}}{\partial r} (r) + \frac{\partial f}{\partial r} (x^{*} (r), r)$ 由一阶必要条件可得 $\nabla_{x} f (x^{*} (r), r) = {[\frac{\partial g}{\partial x} (x^{*} (r), r)]}^{T} λ^{*} (r)$ ，故 $\frac{\partial f^{*}}{\partial r} (r) = λ^{*} (r)^{T} \frac{\partial g}{\partial x} (x^{*} (r), r) \frac{\partial x^{*}}{\partial r} (r) + \frac{\partial f}{\partial r} (x^{*} (r), r)$ 注意到 $\forall r \in R^{k}$ ，恒有 $g (x^{*} (r), r) = 0$ ，令对 $r$ 求导可得 $\frac{\partial g}{\partial x} (x^{*} (r), r) \frac{\partial x^{*}}{\partial r} (r) + \frac{\partial g}{\partial r} (x^{*} (r), r) = 0 ⟹ \frac{\partial g}{\partial x} (x^{*} (r), r) \frac{\partial x^{*}}{\partial r} (r) = - \frac{\partial g}{\partial r} (x^{*} (r), r)$ 代入上式得 $\frac{\partial f^{*}}{\partial r} (r) = \frac{\partial f}{\partial r} (x^{*} (r), r) - λ^{*} (r)^{T} \frac{\partial g}{\partial r} (x^{*} (r), r) = \frac{\partial L}{\partial r} (x^{*} (r), λ^{*} (r), r)$ $◻$

为了进一步探讨 $λ$ 的含义，我们考虑如下带松弛约束的静态优化问题： $max_{x \in Ω} f (x) s.t. g (x) = c ⟹ L (x, λ, c) = f (x) - λ \cdot (g (x) - c)$ 其最优解可记为 $x^{*} (c)$ ，对应的Lagrange乘子和最优目标函数值分别记为 $λ^{*} (c)$ 和 $f^{*} (c)$ 。由包络定理可得 $\frac{\partial f^{*}}{\partial c} (c) = \frac{\partial L}{\partial c} (x^{*} (c), λ^{*} (c), c) = λ^{*} (c)^{T} ⟹ \nabla_{c} f^{*} (c) = λ^{*} (c)$ 由此可见，Lagrange乘子 $λ^{*} (c)$ 表示目标函数值对约束松弛量 $c$ 的敏感度，即约束松弛量 $c_{i}$ 每增加一个单位，目标函数值将增加 $λ_{i}^{*} (c)$ 个单位。在经济学中，约束对应资源限制，Lagrange乘子即反映了资源限制对最优值的边际影响，因此也称为影子价格。

上述含义为我们提供了另一种计算Lagrange乘子的方法： $λ^{*} = \nabla_{c} f^{*} (0)$ ，这种思想在后续带不等式约束的静态优化中起到重要作用。

5.3.3 带不等式约束的静态优化

定义 5.3.18 设开集 $Ω \subseteq R^{n}$ ， $f, g_{i}, h_{j} : Ω \to R$ ， $i = 1, 2, \dots, m$ ， $j = 1, 2, \dots, l$ 。带不等式约束的静态优化问题是指求解 $max_{x \in Ω} f (x) s.t. {\begin{cases} g_{i} (x) \leq 0, & i = 1, 2, \dots, m \\ h_{j} (x) = 0, & j = 1, 2, \dots, l \end{cases}$ 可行域 $S = {x \in Ω ∣ g_{i} (x) \leq 0, h_{j} (x) = 0, i = 1, 2, \dots, m, j = 1, 2, \dots, l}$ 。

我们先定义一些必要的概念。

定义 5.3.19 (起作用约束) 设可行解 $x_{0} \in S$ ，考虑某不等式约束 $g_{i} (x_{0}) \leq 0$ ：

若 $g_{i} (x_{0}) = 0$ ，则称 $g_{i} (x_{0}) \leq 0$ 是在 $x_{0}$ 处的起作用约束；
若 $g_{i} (x_{0}) < 0$ ，则称 $g_{i} (x_{0}) \leq 0$ 是在 $x_{0}$ 处的不起作用约束。

等式约束 $h_{j} (x_{0}) = 0$ 恒为起作用约束。将 $f$ 在 $x_{0}$ 处的起作用约束下标集记作 $I (x_{0})$ 。

定义 5.3.20 (上升方向、可行方向) 设 $x_{0} \in S$ ，若 $d \neq 0$ 满足 $\exists δ > 0$ 使得 $\forall λ \in (0, δ)$ ， $f (x_{0} + λ d) > f (x_{0})$ ，则称 $d$ 为 $f$ 在 $x_{0}$ 处的上升方向。

若 $d \neq 0$ 满足 $\exists δ > 0$ 使得 $\forall λ \in (0, δ)$ ， $x_{0} + λ d \in S$ ，则称 $d$ 为 $f$ 在 $x_{0}$ 处的可行方向。

集合 $F := {d ∣ \nabla f (x_{0}) \cdot d > 0}$ 中的方向均为上升方向。
对于不等式约束，集合 $G := {d ∣ \nabla g_{i} (x_{0}) \cdot d < 0, i \in I}$ 中的方向均为可行方向。
对于等式约束，可能不存在可行方向，故可考虑切空间 $H := {d ∣ \nabla h_{j} (x_{0}) \cdot d = 0, j = 1, 2, \dots, l}$ 中的方向，其中 $x_{0}$ 为约束曲面 $h (x) = 0$ 正则点。

利用上升方向和可行方向的概念，我们可以给出带不等式约束的静态优化问题的一阶必要条件。

定理 5.3.21 (一阶必要条件) 若 $x^{*}$ 是极大值点，且为约束曲面 $h (x) = 0$ 正则点，则不存在 $f$ 在 $x^{*}$ 处的上升方向 $d$ 同时为可行方向，即 $F \cap G \cap H = \emptyset$ 。

利用Motzkin定理⁴，可将一阶必要条件代数化。

定理 5.3.22 (Motzkin定理) 设 $A, B, C$ 为矩阵、 $A \neq 0$ ，记 $> (\geq)$ 表示逐元素大于（等于），以下两个命题择一成立：

$A x > 0, B x \geq 0, C x = 0$ 有解 $x$ 。
$A^{T} y_{1} + B^{T} y_{2} + C^{T} y_{3} = 0$ 有解 $y_{1}, y_{2}, y_{3}$ ，其中 $y_{1} \geq 0, y_{2} \geq 0$ 且 $y_{1} \neq 0$ 。

定理 5.3.23 (一阶必要条件，Fritz John条件) 若 $x^{*}$ 是极大值点，则存在不全为零的 $λ_{0} \geq 0$ 、 $λ_{i} \geq 0 (i \in I)$ 、 $μ_{j} (j = 1, 2, \dots, l)$ 使得 $λ_{0} \nabla f (x^{*}) = \sum_{i \in I} λ_{i} \nabla g_{i} (x^{*}) + \sum_{j = 1}^{l} μ_{j} \nabla h_{j} (x^{*})$

证明记 $I = {i_{1}, i_{2}, \dots, i_{k}}$ ，以及 $A = (\begin{matrix} \nabla f (x^{*})^{T} \\ - \nabla g_{i_{1}} (x^{*})^{T} \\ ⋮ \\ - \nabla g_{i_{k}} (x^{*})^{T} \end{matrix}), B = 0, C = - (\begin{matrix} \nabla h_{1} (x^{*})^{T} \\ \nabla h_{2} (x^{*})^{T} \\ ⋮ \\ \nabla h_{l} (x^{*})^{T} \end{matrix})$ 则一阶必要条件可化为 $\emptyset = F \cap G \cap H = {d \in R^{n} ∣ A d > 0, B d \geq 0, C d = 0}$ 由Motzkin定理可知，存在 $y_{1} = (λ_{0}, λ_{i_{1}}, \dots, λ_{i_{k}})^{T}$ 满足 $y_{1} \geq 0$ 且 $y_{1} \neq 0$ 、 $y_{3} = (μ_{1}, \dots, μ_{l})^{T}$ 使得 $A^{T} y_{1} + C^{T} y_{3} = 0 ⟹ λ_{0} \nabla f (x^{*}) = \sum_{i \in I} λ_{i} \nabla g_{i} (x^{*}) + \sum_{j = 1}^{l} μ_{j} \nabla h_{j} (x^{*})$ $◻$

我们不关心 $λ_{0} = 0$ 的情形，因为此时约束条件（的梯度）线性相关，说明可以用较少的约束条件描述可行域。若 $λ_{0} > 0$ （此时引入正则条件），则可将上式两端同时除以 $λ_{0}$ ，得到KKT条件。

定理 5.3.24 (一阶必要条件，Karush-Kuhn-Tucker条件) 设 $x^{*}$ 为正则点，即 $\nabla g_{i} (x^{*}), \nabla h_{j} (x^{*})$ 线性无关（其中 $i \in I (x^{*})$ ， $j = 1, 2, \dots, l$ ）。若 $x^{*}$ 是极大值点，则存在 $λ_{i} \geq 0 (i \in I)$ 、 $μ_{j} (j = 1, 2, \dots, l)$ 使得 $\nabla f (x^{*}) = \sum_{i \in I} λ_{i} \nabla g_{i} (x^{*}) + \sum_{j = 1}^{l} μ_{j} \nabla h_{j} (x^{*})$

为了将不起作用约束也纳入考虑，我们引入互补松弛条件： $λ_{i} g_{i} (x^{*}) = 0, λ_{i} \geq 0, i = 1, 2, \dots, m$

综合KKT条件与互补松弛条件，可借助Lagrange乘子法，得到带不等式约束的静态优化问题的一阶必要条件：

定理 5.3.25 (一阶必要条件，Lagrange乘子法·KKT条件) 设 $x^{*}$ 为正则点，即 $\nabla g_{i} (x^{*}), \nabla h_{j} (x^{*})$ 线性无关（其中 $i \in I (x^{*})$ ， $j = 1, 2, \dots, l$ ）。定义 $L (x, λ, μ) := f (x) - \sum_{i = 1}^{m} λ_{i} g_{i} (x) - \sum_{j = 1}^{l} μ_{j} h_{j} (x)$ 若 $x^{*}$ 是极大值点，则存在 $λ_{i} \geq 0 (i = 1, 2, \dots, m)$ 、 $μ_{j} (j = 1, 2, \dots, l)$ 使得 $\nabla_{x} L (x^{*}, λ^{*}, μ^{*}) = 0$ ，且成立互补松弛条件： $λ_{i} g_{i} (x^{*}) = 0, i = 1, 2, \dots, m$

同理，在经济学中，这里的 $λ_{i}, μ_{i}$ 也称为影子价格，反映了约束对最优值的边际影响。注意到 $λ_{i}$ 可以是 $0$ ，对应的不等式约束对最优值没有边际影响，此时约束并不起作用，亦即对应的资源不稀缺，由此得到经典名言——不稀缺的资源无边际价值，有边际价值的资源稀缺。

一阶必要条件的几何意义是：在最大值点处，目标函数 $f (x)$ 的等值线与起作用约束曲面的等值线相切，且 $f$ 的上升方向与曲面的法向同向。

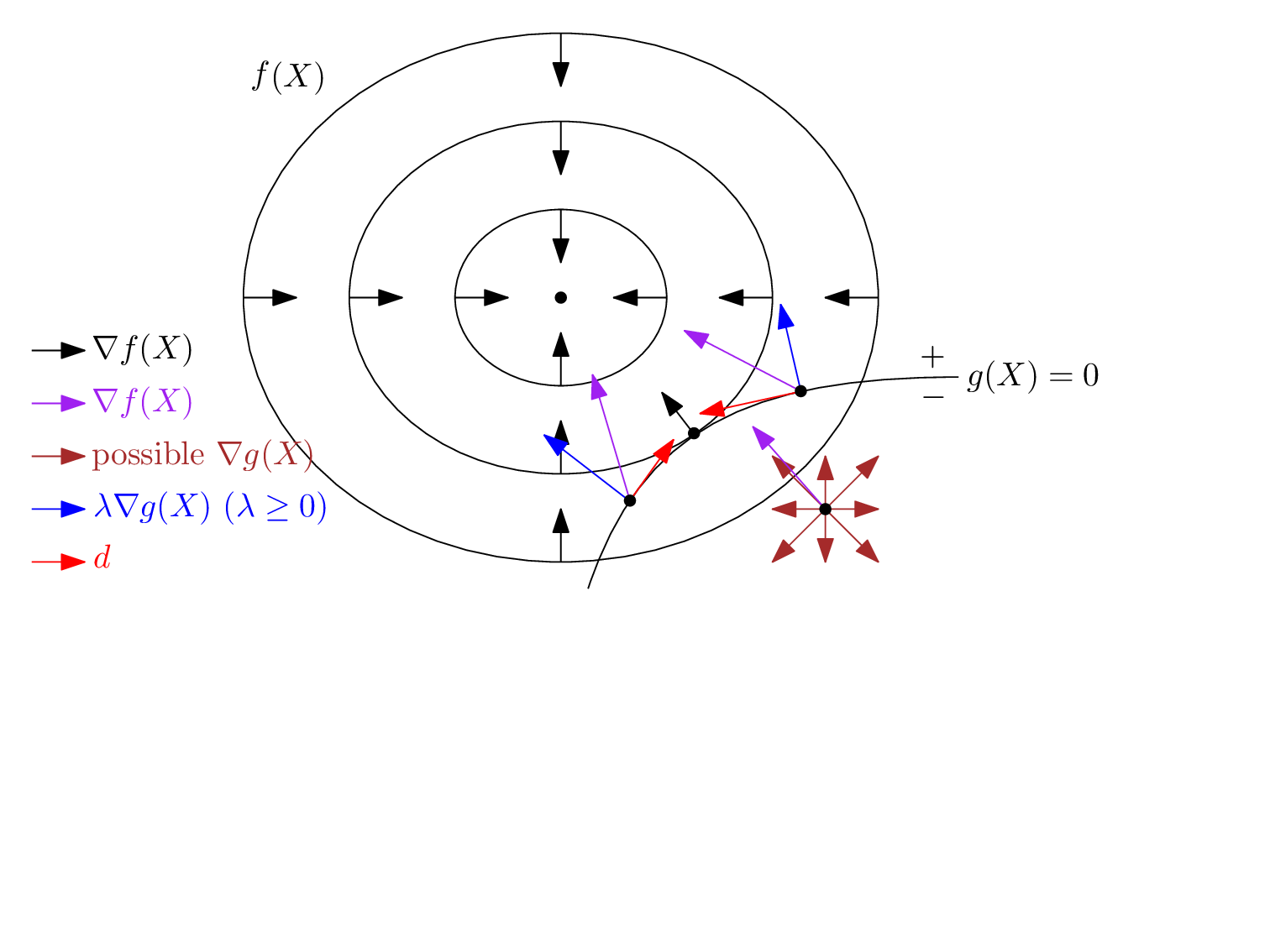
图 5.3.2: 如果上升方向 $\nabla f (x)$ 与起作用约束曲面的法向 $λ_{i} \nabla g_{i} (x)$ 不共线，则切平面存在可行方向 $d$ 使得 $f$ 增大；而 $λ_{i} \geq 0$ 保证了当 $\nabla f (x)$ 与 $λ_{i} \nabla g_{i} (x)$ 共线时，两者同向，此时 $\nabla f (x)$ 不为可行方向，亦即不存在可行方向使得 $f$ 增大。

为了给出一阶充分条件，我们需要限制 $f, g_{i}, h_{j}$ 的性质，由此给出凹规划的概念。

定义 5.3.26 (凹规划) 称以下规划问题为凹规划，若 $f$ 在 $Ω$ 上凹， $g_{i}$ 在 $Ω$ 上凸， $h_{j}$ 为线性函数。容易证明其可行域 $S$ 为凸集。 $max_{x \in Ω} f (x) s.t. {\begin{cases} g_{i} (x) \leq 0, & i = 1, 2, \dots, m \\ h_{j} (x) = 0, & j = 1, 2, \dots, l \end{cases}$

凹规划并未要求 $f$ 可微，故 $f$ 的梯度未必存在。为此，我们引入超梯度的概念：

定义 5.3.27 (超梯度) 称 $λ \in R^{n}$ 为 $f$ 在 $x_{0}$ 处的超梯度，若 $\forall x \in Ω$ ，成立 $f (x) - f (x_{0}) \leq λ \cdot (x - x_{0})$

凹函数的超梯度必定存在。若凹函数 $f$ 在 $x_{0}$ 处可微，则其超梯度存在且唯一，且为 $\nabla f (x_{0})$ 。

为了证明凹规划的一阶充分条件，我们需要计算出不等式约束对应的Lagrange乘子 $λ$ 。利用Lagrange乘子的经济学含义，我们考虑对不等式约束进行松弛，考虑如下带参数的凹规划： $P (c) : max_{x \in Ω} f (x) s.t. {\begin{cases} g_{i} (x) \leq c_{i}, & i = 1, 2, \dots, m \\ h_{j} (x) = 0, & j = 1, 2, \dots, l \end{cases}$ 其中可行域 $S (c) := {x \in S ∣ g (x) \leq c, h (x) = 0}$ 满足 $S (0) \neq \emptyset$ 。上述规划的最优目标函数 $f^{*} (c)$ 在 $c = 0$ 处的（超）梯度 $λ$ 即为我们需要的Lagrange乘子。为了保证超梯度存在， $f^{*}$ 的性质需要足够好（如 $f^{*}$ 凹）。

考虑新的目标函数 $L (x, λ) := f (x) - λ \cdot g (x)$ ，即可消除不等式约束，将问题转化为仅含等式约束的静态优化： $P^{'} : max_{x \in Ω} L (x) s.t. h (x) = 0$ 如果 $P^{'}$ 的最优解与 $P (0)$ 的最优解相同，且 $L$ 的性质足够好（如 $L$ 关于 $x$ 凹），则可利用等式约束的静态优化的一阶充分条件，得到凹规划的一阶充分条件。

记 $C := {c \in R^{m} ∣ S (c) \neq \emptyset}$ ，设 $0$ 为 $C$ 的内点（否则不等式约束退化为等式约束），由此得到下面的定理：

定理 5.3.28

(1): $\forall c \in C$ ，凹规划 $P (c)$ 的最优目标函数 $f^{*} (c)$ 存在。
(2): $f^{*}$ 凹，故 $f^{*}$ 在 $0$ 处的超梯度 $λ$ 存在。
(3): $f^{*}$ 在 $0$ 处的任意超梯度 $λ \geq 0$ 。
(4): 设 $x^{*} (c)$ 为 $P (c)$ 的最优解，则成立互补松弛条件 $λ_{i} g_{i} (x^{*} (0)) = 0 (i = 1, 2, \dots, m)$ 。
(5): $L (x, λ)$ 关于 $x \in Ω$ 凹，故 $P^{'}$ 的一阶充分条件适用。
(6): $P^{'}$ 的最优解与 $P (0)$ 的最优解相同。

证明 (1) $S (c)$ 为非空紧集，连续函数在非空紧集上存在最值，故 $f^{*} (c)$ 存在。

(2) 下证 $f^{*}$ 为凹函数，即 $f^{*} (t c_{1} + (1 - t) c_{2}) \geq t f^{*} (c_{1}) + (1 - t) f^{*} (c_{2}), \forall c_{1}, c_{2} \in C, t \in [0, 1]$ 设 $t \in [0, 1]$ ，记 $c = t c_{1} + (1 - t) c_{2}$ ，注意到 $x_{k} := x^{*} (c_{k}) (k = 1, 2)$ 满足 $g (x_{k}) \leq c_{k}, h (x_{k}) = 0, k = 1, 2$ 由于 $g$ 凸、 $h$ 为线性函数，因此 $x = t x_{1} + (1 - t) x_{2}$ 满足 ${\begin{cases} g (x) \leq t g (x_{1}) + (1 - t) g (x_{2}) \leq t c_{1} + (1 - t) c_{2} = c \\ h (x) = t h (x_{1}) + (1 - t) h (x_{2}) = 0 \end{cases} ⟹ x \in S (c)$ 因此 $x$ 为凹规划 $P (c)$ 的可行解，故有 $f^{*} (c) \geq f (x) \geq t f (x_{1}) + (1 - t) f (x_{2}) = t f^{*} (c_{1}) + (1 - t) f^{*} (c_{2})$ 由此表明 $f^{*}$ 为凹函数，其在 $0$ 处的超梯度 $λ$ 存在。

(3) 下证 $λ \geq 0$ ，由超梯度的定义可得 $f^{*} (c) - f^{*} (0) \leq λ \cdot c, \forall c \in C$ 设 $c_{0} \in C_{0} := [0, + \infty)^{m}$ ，则 $S (0) = {x \in S ∣ g (x) \leq 0, h (x) = 0} \subseteq {x \in S ∣ g (x) \leq c_{0}, h (x) = 0} = S (c_{0}) ⟹ c_{0} \in C$ 亦即与 $P (0)$ 相比， $P (c_{0})$ 的可行域更大、对应更弱的约束，故 $f^{*} (c_{0}) \geq f^{*} (0)$ 。分别取 $c_{i} \in C_{0}$ 满足“第 $i$ 个分量为 $1$ ，其余分量为 $0$ ”，则由超梯度的定义可得 $0 \leq f^{*} (c_{i}) - f^{*} (0) \leq λ \cdot c_{i} = λ_{i}, i = 1, 2, \dots, m$ 故 $λ \geq 0$ 。

(4) 下证互补松弛条件： $λ_{i} g_{i} (x^{*} (0)) = 0 (i = 1, 2, \dots, m)$ ，只需考虑 $λ_{i} > 0$ 的那些不等式约束。由于 $0$ 为 $C$ 的内点，设 $δ > 0$ 满足 $- δ c_{i} \in C$ ，由超梯度的定义可得 $f^{*} (- δ c_{i}) - f^{*} (0) \leq λ \cdot (- δ c_{i}) = - δ λ_{i} < 0 ⟹ f^{*} (- δ c_{i}) < f^{*} (0) = f (x^{*} (0))$ 规划 $P (- δ c_{i})$ 的最优目标函数值 $f^{*} (- δ c_{i}) < f (x^{*} (0))$ ，说明 $x^{*} (0)$ 不为 $P (- δ c_{i})$ 的可行解，亦即 $x^{*} (0) \notin S (- δ c_{i}) ⟹ - δ < g_{i} (x^{*} (0)) \leq 0 \overset{δ \to 0^{+}}{⟹} g_{i} (x^{*} (0)) = 0 ⟹ λ_{i} g_{i} (x^{*} (0)) = 0$ 故互补松弛条件成立。

(5) 下证 $L (x, λ)$ 关于 $x \in Ω$ 凹。设 $t \in [0, 1]$ ，记 $x = t x_{1} + (1 - t) x_{2}$ ，利用 $f$ 凹、 $g_{i}$ 凸、 $λ_{i} \geq 0$ 可得 $\begin{aligned} L (x, λ) & = f (x) - λ \cdot g (x) \geq [t f (x_{1}) + (1 - t) f (x_{2})] - λ \cdot [t g (x_{1}) + (1 - t) g (x_{2})] \\ = t [f (x_{1}) - λ \cdot g (x_{1})] + (1 - t) [f (x_{2}) - λ \cdot g (x_{2})] = t L (x_{1}, λ) + (1 - t) L (x_{2}, λ) \end{aligned} \forall x_{1}, x_{2} \in Ω$

(6) 下证两个规划的最优解相同。记 $P^{'}$ 的最优解为 $x^{†}$ ，其满足 $h (x^{†}) = 0$ ，故 $x^{†} \in S (g (x^{†})) \neq \emptyset$ ，亦即 $g (x^{†}) \in C$ 。注意到 $x^{†}$ 为 $P (g (x^{†}))$ 的可行解，故有 $f (x^{†}) \leq f^{*} (g (x^{†}))$ 由超梯度的定义可得 $f^{*} (g (x^{†})) - f^{*} (0) \leq λ \cdot g (x^{†})$ 再由互补松弛条件可得 $λ \cdot g (x^{*} (0)) = 0$ 因此 $f (x^{†}) - λ \cdot g (x^{†}) \leq f^{*} (g (x^{†})) - λ \cdot g (x^{†}) \leq f^{*} (0) = f (x^{*} (0)) = f (x^{*} (0)) - λ \cdot g (x^{*} (0))$ 因此 $x^{*} (0)$ 亦为 $P^{'}$ 的最优解，两个规划的最优解相同。 $◻$

借助这个定理，我们最终将凹规划转换成带等式约束的静态优化，此时目标函数 $L (λ, x)$ 关于 $x \in Ω$ 还是凹函数，从而得到一阶充分条件：

定理 5.3.29 (凹规划的一阶充分条件·KKT条件) 对于凹规划，设 $(x^{*}, λ^{*})$ 满足互补松弛条件 $λ_{i}^{*} g_{i} (x^{*}) = 0, λ_{i}^{*} \geq 0, i = 1, 2, \dots, m$ 且 $(x^{*}, μ^{*})$ 满足 $L (x, λ^{*}) := f (x) - λ^{*} \cdot g (x)$ 的一阶充分条件 $\nabla_{x} L (x^{*}, λ^{*}, μ^{*}) = 0$ ，其中 $L (x, λ, μ) := L (x, λ) - μ \cdot h (x) = f (x) - \sum_{i = 1}^{m} λ_{i} g_{i} (x) - \sum_{j = 1}^{l} μ_{j} h_{j} (x)$ 则内点 $x^{*}$ 为凹规划的最大值点。换言之，内点 $x^{*}$ 为凹规划的最大值点当且仅当其满足KKT条件。

类似切空间，我们可以定义可行空间的概念，由此给出带不等式约束的静态优化问题的二阶条件。

定义 5.3.30 (可行空间) 约束 $g (x) \geq 0, h (x) = 0$ 在 $x^{*}$ 处的可行空间 $T (x^{*})$ 定义为 $T (x^{*}) = {d \in R^{n} | \begin{aligned} \nabla g_{i} (x^{*}) \cdot d \leq 0, & i \in I (x^{*}) \\ \nabla h_{j} (x^{*}) \cdot d = 0, & j = 1, 2, \dots, l \end{aligned}} = G \cap H \cap {0}$

定理 5.3.31 (二阶必要条件) 若内点 $x^{*} \in S$ 为此规划的极大值点，则 $(x^{*}, λ^{*}, μ^{*})$ 满足KKT条件，且 $H_{x} L (x^{*}, λ^{*}, μ^{*})$ 在 $T (x^{*})$ 上半负定。

定理 5.3.32 (二阶充分条件) 若 $(x^{*}, λ^{*}, μ^{*})$ 满足KKT条件，且 $H_{x} L (x^{*}, λ^{*}, μ^{*})$ 在 $T (x^{*})$ 上负定，则内点 $x^{*} \in S$ 为此规划的极大值点。

证明留作练习。

最后提一类特殊的规划：拟凹规划，其目标函数为拟凹函数，约束函数为拟凸函数。

定义 5.3.33 (拟凹、拟凸) 称函数 $f : Ω \to R$ 为拟凹，若 $\forall x_{1}, x_{2} \in Ω$ ， $t \in [0, 1]$ ，成立 $f (t x_{1} + (1 - t) x_{2}) \geq min {f (x_{1}), f (x_{2})}$ 称函数 $g : Ω \to R$ 为拟凸，若 $- g$ 为拟凹。

简而言之，拟凹（凸）函数只有一个峰（谷），其上（下）水平集均为凸集。如果拟凹（凸）函数可微，则其梯度满足

定理 5.3.34 (拟凹函数的一阶性质) 设 $f : Ω \to R$ 为可微函数，则 $f$ 拟凹的充分必要条件为： $\forall x_{1}, x_{2} \in Ω$ ，若 $f (x_{2}) > f (x_{1})$ ，则 $\nabla f (x_{1}) \cdot (x_{2} - x_{1}) > 0$

拟凹规划的一阶充分条件与凹规划相同。

定理 5.3.35 (拟凹规划的一阶充分条件·KKT条件) 设 $f$ 在 $Ω$ 上拟凹， $g_{i}$ 在 $Ω$ 上拟凸， $h_{j}$ 为线性函数，且 $x^{*}$ 为正则点。内点 $x^{*}$ 为拟凹规划的最大值点当且仅当其满足KKT条件。

证明设 $(x^{*}, λ^{*}, μ^{*})$ 满足KKT条件。 $\forall x \in S$ ， $g_{i} (x) \leq 0$ ，则 $λ_{i}^{*} g_{i} (x) \leq 0 = λ_{i}^{*} g_{i} (x^{*})$ ，由 $λ_{i}^{*} g_{i}$ 拟凸可得 $λ_{i}^{*} g_{i} (x) \leq λ_{i}^{*} g_{i} (x^{*}) ⟹ λ_{i}^{*} \nabla g_{i} (x^{*}) \cdot (x - x^{*}) \leq 0 ⟹ \sum_{i = 1}^{m} λ_{i}^{*} \nabla g_{i} (x^{*}) \cdot (x - x^{*}) \leq 0$ $h_{j}$ 是线性约束，其可以表示为 $h_{j} (x) = \nabla h_{j} \cdot x + c$ ，故有 $h_{j} (x) = h_{j} (x^{*}) = 0 ⟹ \nabla h_{j} (x^{*}) \cdot (x - x^{*}) = 0 ⟹ \sum_{j = 1}^{l} μ_{j}^{*} \nabla h_{j} (x^{*}) \cdot (x - x^{*}) = 0$ 两式相加可得 $[\sum_{i = 1}^{m} λ_{i}^{*} \nabla g_{i} (x^{*}) + \sum_{j = 1}^{l} μ_{j}^{*} \nabla h_{j} (x^{*})] \cdot (x - x^{*}) \leq 0$ 借助KKT条件可得 $\nabla f (x^{*}) \cdot (x - x^{*}) \leq 0$ 假设 $x^{*}$ 不为拟凹规划的最优解，即 $\exists x \in S$ 使得 $f (x) > f (x^{*})$ 。由 $f$ 的连续、拟凹， $\exists v \in \overset{\circ}{B} (0, δ)$ 使得 $f (x) > f (x + v) > f (x^{*}) ⟹ \nabla f (x^{*}) \cdot (x + v - x^{*}) \geq 0$ 因此 $0 \geq \nabla f (x^{*}) \cdot (x - x^{*}) \geq - \nabla f (x^{*}) \cdot v$ 取 $v = - t \nabla f (x^{*})$ ， $t > 0$ 足够小，则有 $\nabla f (x^{*}) \cdot v = - t ∥ \nabla f (x^{*}) ∥^{2} \geq 0 ⟹ \nabla f (x^{*}) = 0$ ，不满足正则条件，故 $x^{*}$ 为拟凹规划的最优解。 $◻$

5.3.4 静态规划的 Big Picture

优化问题

ray 0gray 0约束条件

ray 0gray 0

max_{x \in Ω} f (x)

ray 0gray 0一阶必要条件

ray 0gray 0

x^{*}

为极值点

⟹ \dots

ray 0gray 0一阶充分条件

ray 0gray 0一阶必要条件

+ \dots

ray 0gray 0

⟹ x^{*}

为最值点

ray 0gray 0二阶必要条件

ray 0gray 0

x^{*}

为极值点

⟹

ray 0gray 0一阶必要条件

+ \dots

ray 0gray 0二阶充分条件

ray 0gray 0一阶必要条件

+ \dots

ray 0gray 0

⟹ x^{*}

为极值点

无约束

——

\nabla f (x^{*}) = 0

f

凹

H f (x^{*})

半负定

H f (x^{*})

负定

带等式约束

g (x) = 0

ray 0gray 0

\nabla_{x} L (x^{*}, λ^{*}) = 0

ray 0gray 0

L (x, λ^{*})

关于

x

凹

ray 0gray 0或

f

凹，

g_{i}

线性

ray 0gray 0

H_{x} L (x^{*}, λ^{*})

ray 0gray 0在

T_{g} (x^{*})

半负定

ray 0gray 0

H_{x} L (x^{*}, λ^{*})

ray 0gray 0在

T_{g} (x^{*})

负定

带不等式约束

ray 0gray 0

g (x) \leq 0

ray 0gray 0

h (x) = 0

ray 0gray 0

\nabla_{x} L (x^{*}, λ^{*}, μ^{*}) = 0

ray 0gray 0

λ_{i} g_{i} (x^{*}) = 0, λ_{i} \geq 0

ray 0gray 0拟凹规划

ray 0gray 0

f

拟凹，

g_{i}

拟凸，

h_{j}

线性

ray 0gray 0

H_{x} L (x^{*}, λ^{*}, μ^{*})

ray 0gray 0在

T (x^{*})

半负定

ray 0gray 0

H_{x} L (x^{*}, λ^{*}, μ^{*})

ray 0gray 0在

T (x^{*})

负定

表 5.3.1: 静态优化问题的总结

优化问题	Lagrange函数	切空间/可行空间
带等式约束	$L (x, λ) := f (x) - λ \cdot g (x)$	$T_{g} (x^{}) := {d \in R^{n} ∣ \nabla g_{i} (x^{}) \cdot d = 0, i = 1, 2, \dots, m}$
带不等式约束	$L (x, λ, μ) := f (x) - λ \cdot g (x) - μ \cdot h (x)$	$T (x^{}) := {d \in R^{n} \| \begin{aligned} \nabla g_{i} (x^{}) \cdot d \leq 0, & i \in I (x^{}) \\ \nabla h_{j} (x^{}) \cdot d = 0, & j = 1, 2, \dots, l \end{aligned}}$

表 5.3.2: 带约束优化问题的Lagrange函数与切空间/可行空间

²可以借助顺序余子式判定： $H f (x^{*})$ 负定 $⟹$ 其顺序余子式的符号负正交替；由于 $H f$ 连续，故在某邻域内其顺序余子式的符号保持不变，从而保持负定。

³对于非退化极值点，即 $H_{x} f (x^{*}, r)$ 可逆的极值点，可以借助隐函数定理由 $\nabla_{x} f (x^{*}, r) = 0$ 确定可微的 $x^{*} (r)$ 。

⁴参考：http://benisrael.net/M0TZKIN.pdf。