8.3 习题课讲解
8.3.1 第一型曲线和曲面积分
例 8.3.1 (例1)
设为椭圆,其周长记为 。求。
解1
椭圆的方程可写成,于是
由对称性,。故。
解2
椭圆的参数方程为
于是
所求第一型曲线积分为
例 8.3.2 (例2)
计算螺旋面的面积,其中。
解1
计算可得
因此
解2
利用
例 8.3.3 (例3)
求圆柱面被拋物柱面及平面 所截部分的侧面积(图8.3.1)。

图 8.3.1: 例3示意图
解1(利用第一类曲线积分的几何意义)
把看成定义在平面圆周上的函数的图像到曲线之间的柱面(图8.3.1中深蓝色部分),计算可得
解2(第一类曲面积分)
曲面在柱坐标系下的参数方程为
计算可得
因此
于是
解3(第一类曲面积分)
由对称性,只求曲面在的部分,此时曲面可以看成函数的图像,定义域为。计算可得
8.3.2 第二型曲线积分
例 8.3.4 ( )
计算:
其中是曲线(),从轴正方向看去为逆时针方向。
)
计算:
其中是曲线(),从轴正方向看去为逆时针方向。
证明
首先需要利用对称性。观察到曲线关于平面对称,在对称点上(以及)大小相等、符号相反(见图 8.3.2),故有

图 8.3.2: 曲线的对称性示意图
其次,本题的关键在于选择合适的曲线参数化方式。一种自然的想法是利用,故可取
计算可得
另一种想法是利用球坐标,即
因此曲线可参数化为
其余计算过程与前述相同。
例 8.3.5 (例4)
设为正向闭曲线,计算:
解
原积分可化为
分四段进行积分可得
例 8.3.6 (例5, )
求
其中是球面片的边界曲线,绕向量按右手定则旋转。
)
求
其中是球面片的边界曲线,绕向量按右手定则旋转。
解
利用Stokes公式并不是一个好的做法,因为3段积分曲线分别在3个坐标平面上,直接计算并不麻烦。利用的轮换对称性可得
其中分别为在坐标平面的部分。对于,计算可得
例 8.3.7 (例6)
设,,为直角坐标平面的第一象限中由直线、和曲线、在所围成的平面有界区域的正向边界(图8.3.3),计算
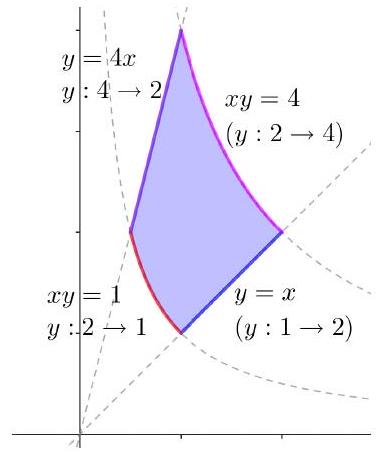
图 8.3.3: 例6示意图
解
边界曲线:
边界曲线:
边界曲线:
边界曲线:
所以
这个证明只需要连续。
例 8.3.8 (例9)
设是正值连续函数,为圆心在原点的单位圆,为的正向边界,证明:
-
(1)
-
-
(2)
-
解
(1) 在第二型曲线曲面积分中,换元的行列式为,这导致曲线、曲面定向发生改变,所以
(2) 由(1)的证明知
例 8.3.9 (例10, )
设在上半平面内,函数具有连续偏导数,且对任意的都有。证明:对内的任意分段光滑的有向简单闭曲线,都有
)
设在上半平面内,函数具有连续偏导数,且对任意的都有。证明:对内的任意分段光滑的有向简单闭曲线,都有
证明
不妨设为自然正向,记围成的区域为。由于在上半平面内,故有
因此
设的原函数为,则有
这个证明只需连续。


