9.2 知识点复习
9.2.1 Green公式
重要概念回顾
-
(1)
-
旋度:平面向量场的旋度定义为。
-
(2)
-
散度:平面向量场的散度定义为。
-
(3)
-
楔积:定义楔积算符为:
- 双线性:。
- 反对称性:。
- 若的边界为自然正向,则。
-
(4)
-
外微分:定义作用在微分形式上的外微分算符为:
重要定理回顾
-
(1)
-
Green公式的物理表述:设为平面闭区域,其边界分段且前向为自然正向,为向量场,则有
- 散度形式:。
- 旋度形式:。
-
(2)
-
Green公式的数学表述:,其中为一阶微分形式。
-
(3)
-
Green公式的展开形式:
应用
-
(1)
-
旋度的物理定义:。旋度为零的场称作无旋场。
-
(2)
-
散度的物理定义:。散度为零的场称作无源场。
-
(3)
-
对于线性向量场,,。
-
(4)
-
计算:,其中为上的椭圆弧,从逆时针旋转到,。
注
-
(1)
-
借助,则旋度和散度可表示为、。
-
(2)
-
注意到,表明散度与坐标系的选取无关。
-
(3)
-
可以验证:
9.2.2 恰当方程与积分因子
我们主要研究以下方程:
称以上方程为恰当方程,若存在,使得
此时原方程的通解为,其中为任意常数。判定恰当方程只需要验证无旋条件是否成立:
如果原方程不是恰当方程,则可以引入积分因子,使得
为恰当方程。此时,应满足
通常情况下,求解以上关于的方程并不会比求解原方程更简单,但是有时候可以通过观察得到的形式(如只与有关等),因为我们只需要的一个特解。
在已知方程恰当后,如不便凑出全微分,可以通过直接积分的方法求解。设恰当方程
则方程的通解满足
其中起点、路径可以任意选择,比如沿折线段、沿线段等。
9.2.3 第二型曲面积分
第二型曲面积分作用在中的曲面上:
作用的函数是一个向量场,其物理意义是通量,如图9.2.1所示。
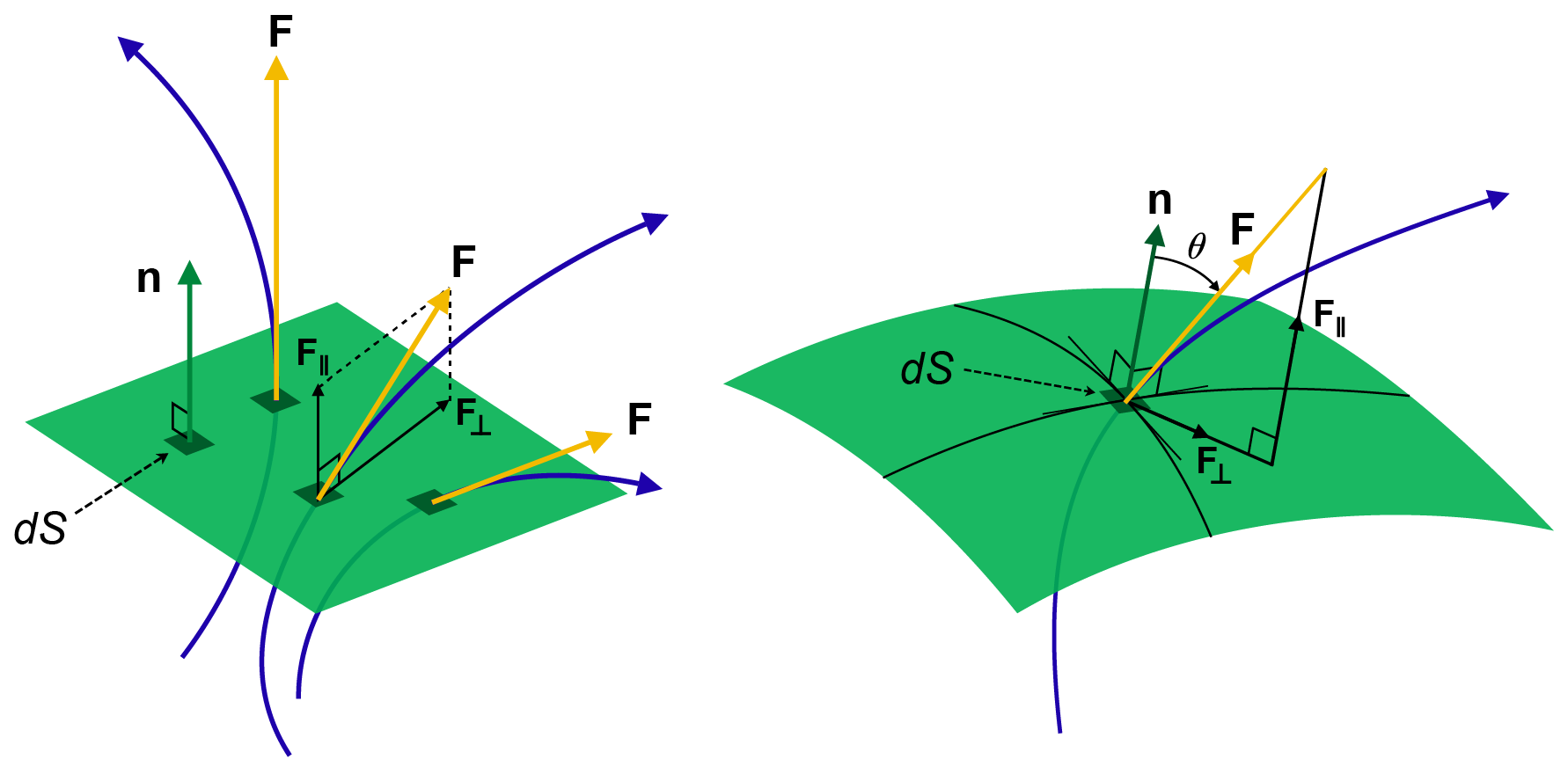
图 9.2.1: 第二型曲面积分的物理意义
重要概念回顾
-
(1)
-
可定向曲面:称曲面是可定向曲面,若的法向量场是连续的。
-
(2)
-
第二型曲面积分:设是可定向曲面,向量场连续,则沿曲面的第二型曲面积分定义为
注意到
因此
上式的物理意义如图9.2.2所示,为构成的(微元)平行六面体的体积。
-
(3)
-
楔积与外微分:在直角坐标系中,定义
则有。设,则原积分可改写为
其中称作二阶微分形式。
楔积的几何意义如图9.2.3所示。如果法向量在上的投影与同向(即),则,其余情况同理。
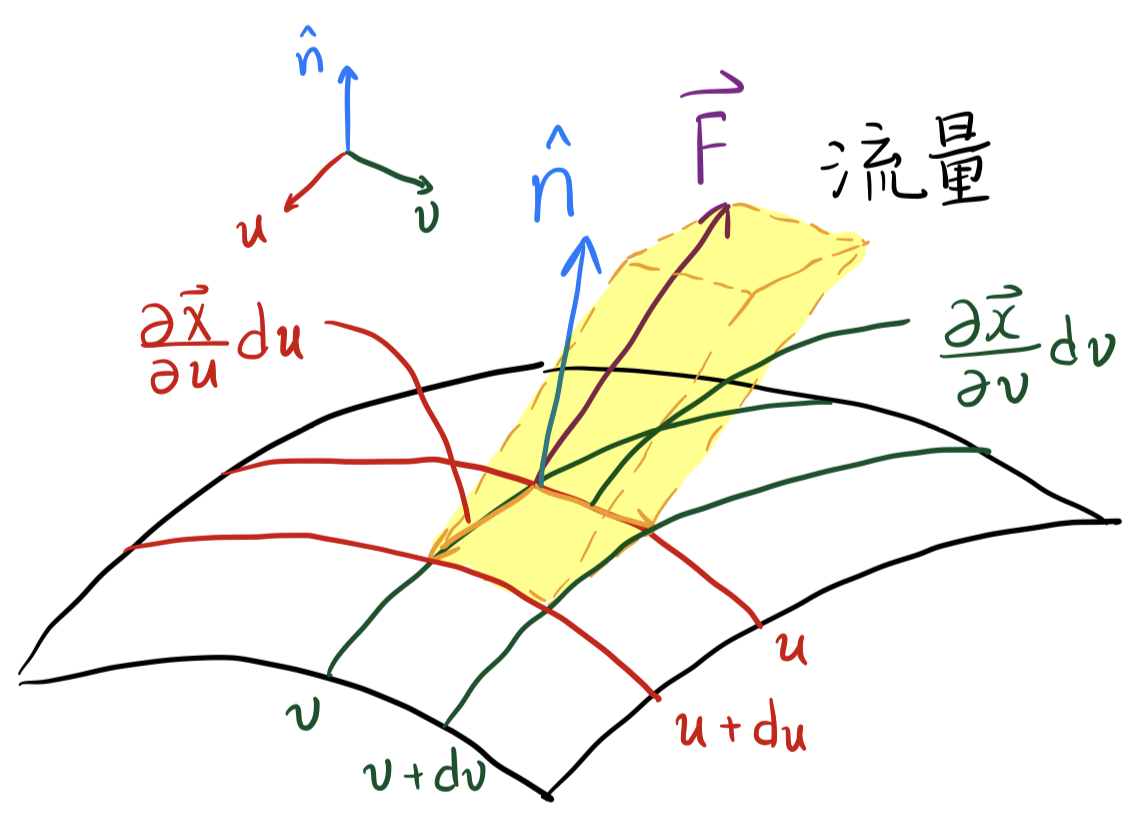
图 9.2.2: 第二型曲面积分的物理意义
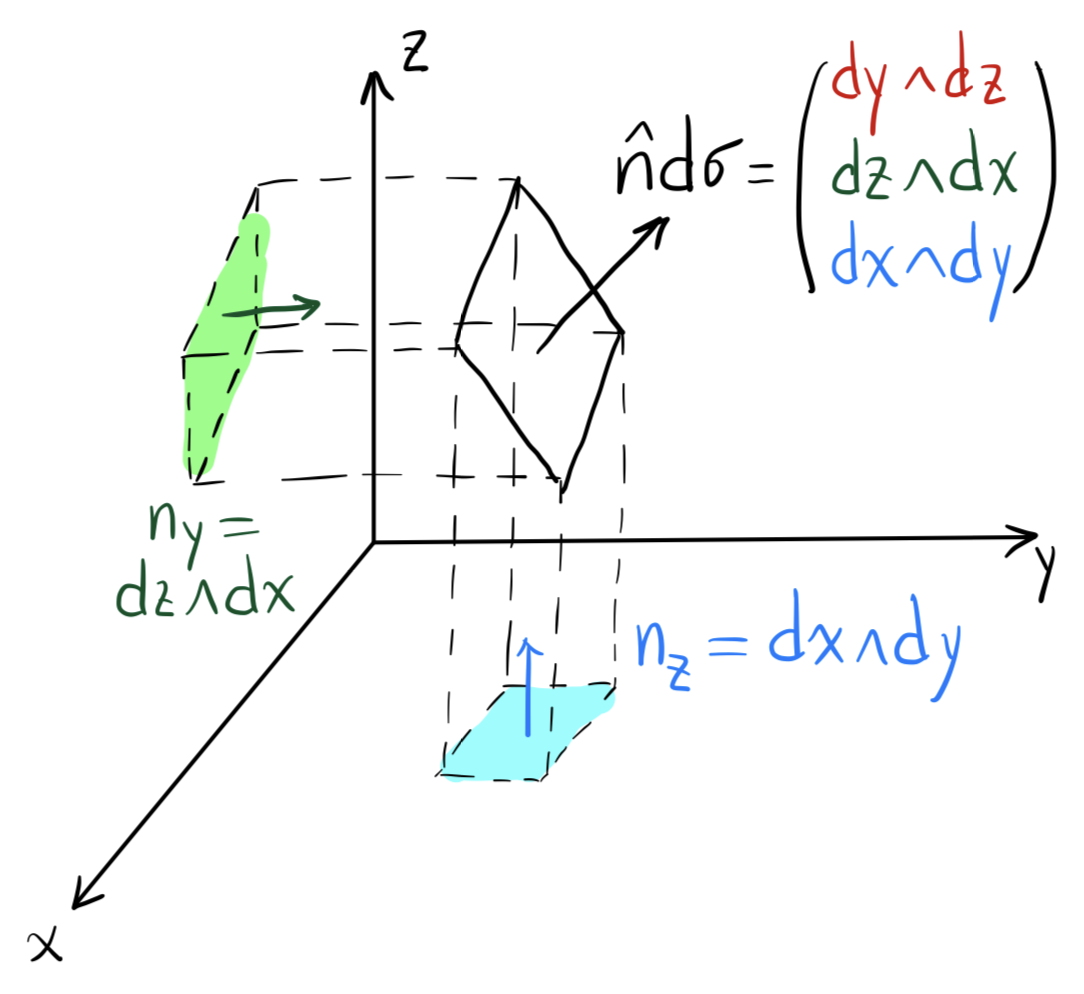
图 9.2.3: 楔积的几何意义
重要定理回顾
第二型曲面积分关于满足线性,关于满足可加性。
应用
-
(1)
-
球面是可定向的,轮胎面是可定向的,Möbius带是不可定向的。
-
(2)
-
设曲面,法向量的分量指向方向,计算:。
-
(3)
-
设曲面,法向量朝外,证明:。
-
(4)
-
设曲面,的分量指向方向,计算:。
注
由于,因此参数的顺序不能随意交换。以球面的参数化(球坐标系)为例,如果为球面外法向量,则应有


